Preliminary Course
Applied Mathematics
Useful parametric functions
A parametric function is written under the generic form f(x,p) where x is a vector of state variables and p is a vector of parameters.
Parametric growth functions
-
In the development of living organisms, measurements of growing organs have often revealed a sigmoid-like shape,
with a slow initiation, a quasi-linear growth phase, and a saturation phase at the termination of expansion once
physiological maturity is reached or once resources are exhausted.
Biologists are interested in quantifying the growth patterns with a few parameters.
To this end, a corpus of parametric functions, also called growth functions, have been developed to represent such dynamics: among others, we can cite
-
the Gompertz function (1825),
the Verhulst function (1838),
the Weibull function (1959),
the Richards function (1959),
the symmetrical expolinear function (Goudriaan, 1994),
or the beta density function (Johnson and Leone, 1964).
The following figure shows the shapes of these functions, used to model a plant mass evolution. The table presents the function equations.
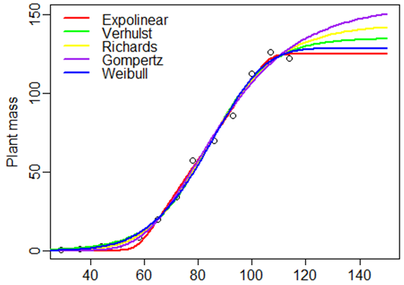
Comparison of several parametric growth functions to model plant mass evolution (dots)
- Gompertz, Verhulst, Weibull, Richards, and symmetrical expolinear functions
| Function | Equation |
| Gompertz (1825) |  |
| Verhulst (1838) | 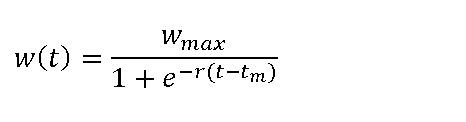 |
| Weibull (1959) | 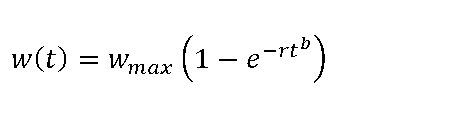 |
| Richards (1959) |  |
| Symmetrical expolinear (Goudriaan, 1994) | 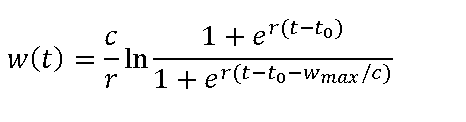 |
| Beta density (Johnson and Leone, 1964) | 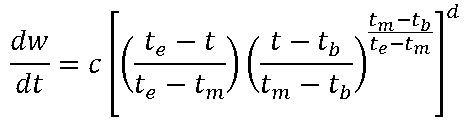 |
Parametric growth functions and their equations.
