Preliminary Course
Applied Mathematics
Formalism of dynamic systems
Dynamic systems
-
A definition of dynamic systems: a little bit of systems theory
In 'General systems research: quo vadis? ' (General Systems: Yearbook of the Society for General Systems Research, Vol.24, 1979, pp.1-9), the famous British scientist in systems theory, Brian R. Gaines, writes the following definition of a system:
"A system is what is distinguished as a system. (...) Systems are whatever we like to distinguish as systems (...).
What then of some of the characteristics that we do associate with the notion of a system, some form of coherence and some degree of complexity?
The Oxford English Dictionary states that a system is a group, set or aggregate of things, natural or artificial, forming a connected or complex whole.
[Once] you have a system, you can study it and rationalize why you made that distinction, how you can explain it, why it is a useful one.
However, none of your post-distinction rationalization is intrinsically necessary to it being a system.
They are just activities that naturally follow on from making a distinction when we take note that we have done it and want to explain to ourselves, or others, why".
According to that definition, a system is characterized by our ability to discriminate between what is part of the system from what is not.
System characterization (Drawing V. Letort-Le Chevalier, ECOLE CENTRALE PARIS)
Dynamical systems are mathematical objects used to model systems whose state (or instantaneous description) changes over time.
They can be continuous or discrete, depending on whether time is considered as a continuous (t ∈ ℜ) or a discrete variable (tn ∈ N ); stochastic or deterministic, depending on whether random effects are considered or not.
Discrete dynamic systems
-
Mathematical definition of discrete dynamic systems
-
A discrete dynamic model M(p) consists of two elements that can be written under the following generic form:
- A set of equations, denoted by f, describing the system behaviour, i.e. the transition from its current state at time n to the following one:
- Xn+1 = f(n, Xn, Un, P)
where Xn ∈ ℜ nx represents the vector of state variables of size nx that characterizes the system at time n, X0 being the initial conditions;
Un ∈ ℜnu is the vector of control variables, of size nu, that characterizes the external factors or stimuli that are applied to the system at time n,
P ∈ ℜnp is the vector of the model parameters, of size np, i.e. a set of constants that characterizes the model behaviour.
- A set of observation functions describing the relationships between the state variables and the model output Y ∈ ℜno that correspond to the vector of available discrete time measured quantities:
-
Y(ns, Uns, P) = g (ns, Xns(Uns, ns, P)
for each sampling time ns with s = 1, ..., Ns
where Xns and Uns are respectively standing for the state variable and control variable at sampling time ns.
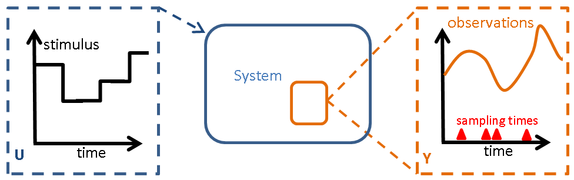Components of a discrete dynamic system (Drawing V. Letort-Le Chevalier, ECOLE CENTRALE PARIS)Bibliography
Gaines B.R. 1979. General systems research: quo vadis ? In: General Systems: Yearbook of the Society for General Systems Research. Vol.24, 1979, pp.1-9.