Preliminary Course
Applied Mathematics
Discrete dynamic systems
Discrete Dynamical Systems Example
-
A growth model
In a plant growth model M(P),
- The state variables can be for instance the amount of biomass produced at time n, the blade area or their nitrogen content.
- The set of parameters P can be considered as genetically determined.
- The environment constraints and the cultural practices (water or nutrient inputs, etc. ) are included in the vector of control variables U.
- The output variables Y are some observables that can be measured on the plant such as the plant architecture or organ sizes.
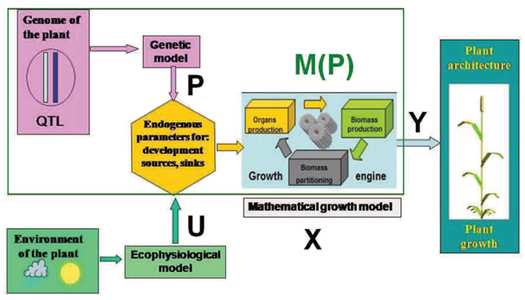
A plant growth model seen as a discrete dynamic system (Drawing V. Letort-Le Chevalier, ECOLE CENTRALE PARIS)
Equilibrium state(s)
-
Definition.
-
A state Xeq is a controlled equilibrium state of a dynamic system if it exists a constant
control variable Ueq such that:
- Xeq = f (n, Xeq, Ueq, P )
An equilibrium state is said to be stable if Xn stays in the neighbourhood of Xeq for any time n, if it is initially in that neighbourhood.
The number and the types of equilibrium states of a dynamic system can depend on the values of its parameter vector.
Exercise
-
A very simple plant growth model.
-
In a very simple model of plant growth, the daily biomass production at day n, Qn is computed as a
function of the leaf area index (LAI) that intercepts a part of the photosynthetically active radiation (PARn) at day n
according to the Beer-Lambert law with a coefficient of interception k and converts it to biomass with a biological efficiency μ.
The leaf area index (LAI) is assumed to be simply a fixed proportion α of the total produced biomass:
Qn+1 = μ PARn (1 - exp (-k * α Qn) )
The initial biomass (seed) is Q0 = 1.
Every day, the total shoot biomass is computed as a fixed proportion with coefficient beta of the total produced biomass:
Shootn = β Qn

A simple growth model (Drawing V. Letort-Le Chevalier, ECOLE CENTRALE PARIS)
Chose the correct proposals and validate
See solutions
