GreenLab Course
Development
Optimizing dual scale production
For a given cycle t, meristems of the same age and physiological age may produce the same pattern in a plant architecture.
In other words, the dual scale automaton will produce similar productions arising from similar macro-states.
In the GreenLab model, the automaton productions are indexed, computed once, and instantiated if allready computed, avoiding this redundancy.
Sub-Structures
-
Similar patterns derived from organogenesis are called Sub-structures.
-
In fact, all ramifications occurring at time ta from a set of identical micro-states
share the same fate at a given date ts.
Therefore, by definition, a given substructure Sp,ta(ts) is classically indexed by a physiological age p, and by two times corresponding respectively to the sub-structure appareance growth cycle ta (the date its first phytomer appears), and the current simulation time ts (the age of the tree expressed in growth cycles).
The value ts - ta is thus the age of the substructure.
Computationally, substructures are defined recursively from the higher physiological stage (i.e. from the smaller pattern) to the lower (i.e. fot the whole plant).
Since the number of physiological ages is limited, as well as the number of micro-states and macro-state transitions, the combinatory of sub-structures is also limited.
It can be shown that their number is linear in time (proportional to ts).
Substructures make the GreenLab approach very efficient for computing plant architecture, since similar patterns are not computed again, or stored, a single representative is stored, and the others just refer to it.
However, plant 3D representations (required for instance for visualisation) still need to instance all sub-structures, exploring each substructure, the sored one, and also each reference of it, with different geometrical positions and orientations.
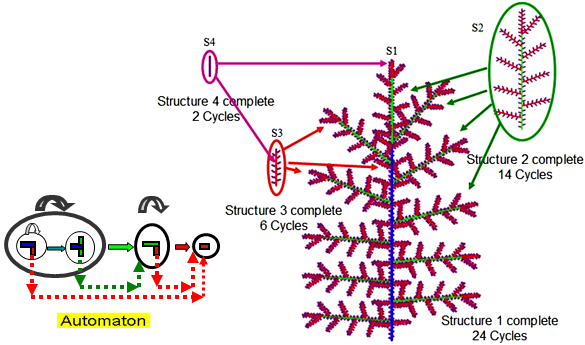
Sub-structures on a simulated determinate plant aged 24 at the end of is growth
- (Images X. Zhao, M.G. Kang, LIAMA, CASIA, and P. de Reffye, CIRAD)
The dual scale automaton is on the left.
In this example, all axes show determinate growth.
In this case, all structures of a given physiological age are identical.
Sub-Structure S4, carries leaves of physiological age 3, and contains 2 phytomers.
Sub-Structure S3, carries 6 S4 sub-structure plus 12 phytomers.
Sub-Structure S2, carries 7 S3 sub-structure and two S4 sub-structures plus 18 phytomers.
Sub-Structure S1, carries 11 S2 sub-structure plus 22 phytomers.
The storage requirement is thus 2+(6+12)+(9+18)+(11+22)=81 elements,
instead of 11*(9*(6*2+12)+18)+22=2596 phytomers.
Definition
[an error occurred while processing this directive]
Bibliography
Yan H.-P., Barczi J.-F. , de Reffye P., and Hu B.-G. 2002. Fast Algorithms of Plant Computation Based on Substructure Instances. International Conferences in Central Europe on Computer Graphics, Visualization and Computer Vision 3/10 (2002) pp. 145-153 (access to paper and pdf)
