Applications
Fitting
Plant structure fitting - Mortality
Retrieving mortality laws
-
Axis mortality, more precisely meristem viability, is a key point in structure development, and is usually easy to see in field measurements
Branched axis mortality increases gradually on the phytomers along the axis, until death occurs if the axis is long enough.
The number of branched dead axes (i.e. with a dead terminal bud) thus increases along the bearing axis from top (tip) to bottom.
This death rate is classically measured on a plant population by a percentage defined from the ratio of dead axes to the total number of axes. This rate increases with the age of the axis.
-
Remember that the age can be retrieved from the branching position (the rank) on the bearer.
For instance, on the coffee tree, one can define an average age i expressed in growth cycles for the phytomer located at rank K from the crown top defined as = K / b1, with b1 standing for the Bernoulli parameter modelling stem development.
Death rates can be fitted to a classic sigmoid function, thus leading to expression of the meristem's viability along the axis as a function of the number of growth cycles.
S(i) = 1 - exp ( -α . iβ)
the mortality probability is :
ci = exp ( -α . ( (i-1)β - (i-2)β ) )
and the death rate at cycle i is given by:
P(i) = exp ( -α . (i-1)β ) - exp ( -α . i β )
Example. Coffee tree branches
-
In axis fitting applications, mortality modelling must be performed after development,
since its expression is a function of the bearing phytomer age.
-
In our Coffea canephora studies, the average number of cycles at rank K was
N = K / b1 with b1 = 0.92.
Measurements were taken for 5 growth cycles on 600 axes for each cycle.
The dataset table and the fitted sigmoid function are given below:
| Rank (K) | 0 | 10 | 15 | 20 | 30-35 |
| Growth cycles (i) | 0, | 14, | 22, | 32, | 47 |
| Death rate (in %) | 0.0, | 0.032, | 0.081, | 0.321, | 0.89 |
The least square regression gives:
- S(i) = 1 - exp ( -8.9 . 10-8 . i4.42) (R=0.999)
The related viability at cycle i is :
1 - ci = exp ( -8.9 . 10-8 .(( i-1)4.42 - ( i-2)4.42))
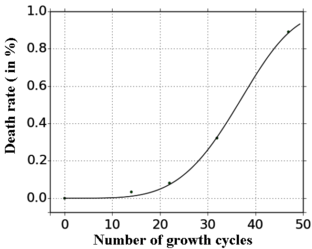
Death rate versus growth cycle (Graph P. de Reffye, CIRAD)
-
The points are data observed at 6 growth stages given in the above table.
The curve stands for the fitted equation: S(i) = 1 - exp ( -8.9 . 10-8 . i4.42) (R=0.999)
