GreenLab Course
Development
Stochastic axis viability modelling
-
Apical bud delays, corresponding to Bernoulli process trial failures in our modelling,
slow down axis growth, but do not stop it. Terminal meristem death may appear at any cycle,
stopping axis development irremediably.
The introducing of a death process, called mortality, leads to dead axes distributions being
distinguished from living axes.
A simple mortality case
-
Mortality without development delays
-
Let us first suppose that axis development shows no delays (rhythm ratio set to 1, and probability of
phytomer occurrence for each cycle also set to 1, i.e. w = 1; b = 1.
Let us then consider a distribution of living axes of K cycles, born from terminal buds whose survival probability - also called viability - is c.
Then, the probability of staying alive in the next cycle is: cK+1, and thus the probability of becoming a dead branch is: (1 - c) . c K
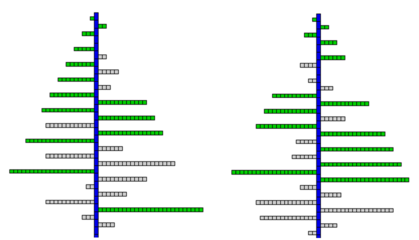
Simulating terminal bud viability on a physiological age 2 axis (Images P. de Reffye, CIRAD)
- 2 simulation examples with viability set to 0.95
Dead axes are shown in grey
Living axes are drawn in green
The retrieval of viability c in this theoretical case can simply be assessed from the ratio of living and dead axes.
Mortality with development delays
-
Let us now consider the usual case with development delays where a new phytomer may appear according to a Bernoulli
process with a probability b , and a viability c.
The probabilities of staying alive or die at cycle K are unchanged, cK+1 and (1 - c) . c K respectively.
This law is a truncated geometric distribution law, whose expected value MN and variance VN are respectively
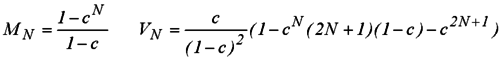(Eq. 1)However, the number of phytomers in a given axis of N cycles becomes complex, since the law is a composition of this geometric law and the binomial B(N,b) law.
The probability of an axis of N cycles having K phytomers is:
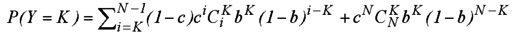
The expected value and variance are then M = MN . d and V = b . (1 - b) . MN + b2 . VN with MN and VN as defined in (Eq. 1) giving finally:
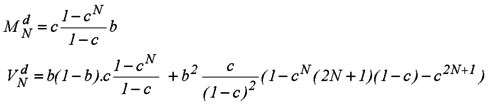
A generic mortality law
-
We have seen that the death rate, or viability, when constant, can be retrieved from measurements on the living
and dead axis statistics for given growth cycles.
However, in many cases this viability rate is not stable with the age of the axis, i.e. with the number of cycles.
-
In most cases, the mortality law is complex, following a sigmoid function shape.
It is thus interesting to fit cumulated dead populations to a classic sigmoid function, leading thus to expressing meristem's viability along the axis as a function of the number of growth cycles, such that:
S(i) = 1 - exp ( -α . iβ)
Viability can then be expressed as:
ci = exp ( -α . ( (i-1)β - (i-2)β ) )
and the death rate at cycle i is given by:
P(i) = exp ( -α . (i-1)β ) - exp ( -α . i β )
See fitting page ( ../App/GLapp_fitst_016.html ) as an example.