Preliminary Course
Applied Mathematics
Usual Parametric functions
Negative exponential function
-
In many plant growth models, (e.g. Pilote, Ceres, STICS, GreenLab), the biomass production at time t, Q(t), is expressed as a parametric function of the leaf area index, the LAI (the one-sided green leaf area per unit ground area, expressed in m2.m-2, so dimensionless). μ stands for a positive proportional coefficient.
Q(t) = μ . ( 1 - e -k LAI(t))
This expression assumes that biomass production is determined by the amount of radiation that is intercepted by the plant/field and can be derived from the Beer-Lambert law, an empirical relationship between the absorption of a monochromatic light wave in an isotropic and homogeneous medium to its concentration.
The parameter k drives the curve variation. μ is a real positive value standing for a biological efficiency factor.
Note that more than 95% of the incoming radiation is intercepted when LAI ≥ -ln(0.05)/k, i.e. when LAI ≥ ≈ 3 if k = 1.
Above that value, increasing the LAI has nearly no effect on the production (phenomenon of 'LAI saturation').
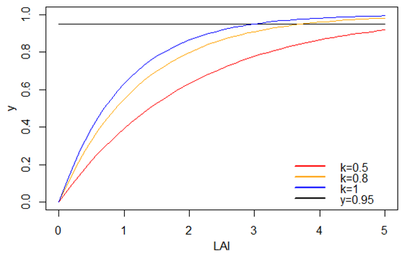
Biomass production as a function of LAI (graph V. Letort- Le Chevalier, ECOLE CENTRALE PARIS)
y stands for the production Q(t)
Exercise
-
Let the function f be defined as f(x) = μ . (1 - e-k.x) with μ = 3.
What is the value of k given that:
-
the derivative of f at x = 0 is equal to 2.25 ?
f(x) reaches 97% of its supremum (least upper bound) at x = 6 ?
Bibliography
Mailhol, J. and Gonzalez, J. 1993. Furrow Irrigation Model for Real-Time Applications on Cracking Soils. Journal of Irrigation and Drainage Engineering, 1993, 119:5, pp. 768-783
CERES:Jones, C.A., and J.R. Kiniry. 1986. CERES-Maize : a simulation model of maize growth and development. Edited by C.A. Jones and J.R. Kiniry. College Station : Texas A&M University Press, 1986. 194 p.
Stics:Brisson, N.,Gary, C., Justes, E., Roche, R., Mary, B., Ripoche, D., Zimmer, D., Sierra, J., Bertuzzi, P., Burger, P., Bussière, F. Cabidoche, Y.M., Cellier, P., Debaeke, P., Gaudillère, J.P., Hénault, C., Maraux, F., Seguin, B., Sinoquet, H. 2003. An overview of the crop model stics, European Journal of Agronomy, Volume 18, Issues 3-4, January 2003, Pages 309-332, ISSN 1161-0301
GreenLab:Kang, M.G., Cournède, P.H., Mathieu, A., Letort, V., & Qi, R. 2009. A Functional-Structural Plant Model: Theories and its Applications in Agronomy. Cao, W. and White, J. and Wang, E. Crop Modeling and Decision Support, Springer, pp. 148-160, 2009, 978-3-642-01131-3
