Preliminary Course
Applied Mathematics
Beta density functions
The beta density function
-
The beta density function has some advantages, as described by Yin (2003)
-
- at initial time t = 0, its value is zero (as for the Weibull function)
- the values of the final growth rate is null, which means that the expansion duration is finite.
- it has a high flexibility and can describe asymmetric growth trajectories (as Richards law)
- it has stable parameters for statistical estimation (similar to Gompertz or logistic functions)
Different parameterizations of the beta density function can be found.
-
In this course, we opt for the following one that depends only on three parameters a, b and Te,
and we use a discretized form:

and dw/dt(t) = 0 elsewhere.
N is a multiplicative factor introduced to normalize the function so that its maximum is equal to 1:
The following figures represent different shapes of beta density function, for several values of parameters a and b, and the shape of the integrated function (the 'growth function').
Note how asymmetrical shapes can be obtained when a ≠ b.
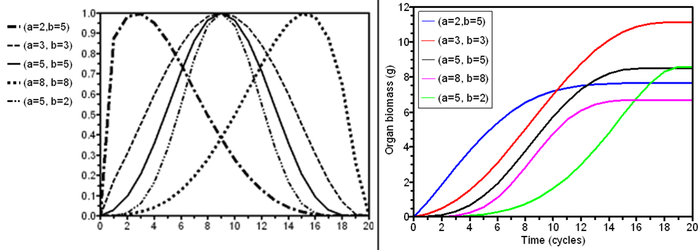
Beta density functions and their respective integrated functions
