GreenLab Course
Development
Factorisation
Substructure construction
Buds, Phytomers and Substructures
-
From the botanical description of the plant, we know that phytomers and buds are the elementary bricks of
plant structure.
They are derived from buds and build the axes.
Let P be the maximum number of physiological ages in the plant.
In practice, P is generally small (P < 5).
At growth cycle t, a metamer (i.e. a micro-state) is characterized by its physiological age p, and the physiological age of its axillary branches q, with q <= p, and its chronological age n.
It is denoted by mtp,q(n).
These three indices p, q, and n are sufficient to describe all the phytomers and their number grows linearly with t.
A bud is only characterized by its physiological age p and is denoted by sp.
The terminal bud of a plant axis produces different kinds of metamers bearing axillary buds of various physiological ages. These buds themselves give birth to axillary branches and so on.
A sub-structure is the complete plant structure that is generated after one or more cycles by a bud.
In the deterministic case, all the subestructures with the same physiological and chronological ages are identical if they have developed at the same moment in the tree architecture.
At cycle t, a sub-structure is thus characterized by its physiological age p and its chronological age n.
It is denoted by Stp(n).
Since the physiological age of the main trunk is 1, at growth cycle t, the sub-structure of physiological age 1 and of chronological age t, St1(t),represents the whole plant.
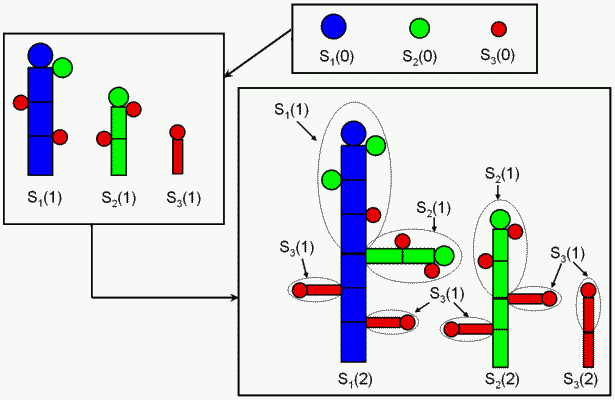
Subestructures encoding (Drawings C. Loi, P.H. Cournède, ECOLE CENTRALE PARIS)
- Factorizing plant development and its subestructure inductive construction: example
for a plant off three physiological ages.
Blue, green and red are respectively the colours corresponding to physiological age 1, 2 and 3.
Circles materialize the buds, while rectangles the phytomers.
S1(2), while S2(2) and S3(2) are substructures of age 2 at physiological ages 2 and 3, respectively. They may both appear in the tree at chronological age 3.
The total number of different sub-structures in a plant of chronological age t is very small, usually fewer than 30, even if the total number of organs is high.
Sub-structures and phytomers are repeated many times in the tree architecture, but they need to be computed only once for each kind.
The sub-structure construction equation
-
The concatenation operator to describe the organization of plant phytomers and sub-structures
and deduce their construction at growth cycle t by induction is as follows:
- Sub-structures of chronological age zero are buds:
Stp(0) = sp - If all sub-structures of chronological age n - 1 are built, we deduce the sub-structures
of chronological age n as:
Stp(n) = [ ∏p≤q≤P ( mtp,q(n) )up,q(t+1-n) ( Stq(n-1) )bp,q(t+1-n) ] Stp(n-1) (equation 6)
for all (p,q) such as p ≤ P and (p ≤ q ≤ P)
where
-
up,q corresponds to the number of metamers mp,q(t) in growth units of
physiological age p appearing at growth cycle t
bp,q corresponds to the number of axillary sub-structures of physiological age q in growth units of physiological age p that appeared at growth cycle t
These sequences can be deterministic or stochastic.
This construction equation is used to count the metamers of each sub-structure.
Formula interpretation
|
∏p≤q≤P ( mtp,q(n) )up,q(t+1-n)
stands for the existing old phytomers on the substructure main axis (the base growth unit) ∏p≤q≤P ( Stq(n-1) )bp,q(t+1-n) stands for the lateral substructures borne by the base growth unit (they are one cycle younger) Stp(n-1) stands for the substructure grown from the apical bud of the base growth unit (also one cycle younger). |
 (Drawing M. Jaeger, CIRAD) |
Note
∏ is the product operator, used in mathematics to represent the product of a bunch of terms. ∏k=2,5(k) = 2 x 3 x 4 x 5 = 120
Bibliography
Yan H.-P., Barczi J.-F. , de Reffye P., and Hu B.-G. 2002. Fast Algorithms of Plant Computation Based on Substructure Instances. International Conferences in Central Europe on Computer Graphics, Visualization and Computer Vision 3/10 (2002) pp. 145-153 (access to paper and pdf)
